実用数学技能検定(以下、数学検定と略す)は公益財団法人日本数学検定協会が実施する算数・数学の技能を測る記述式の検定であり、幼児から大学・一般レベルまで全15級の幅広い階級から構成されています。
個人の数学の技能を測ることはもちろんですが、それ以外にも検定に合格することで、学校によっては中学・高校・大学等の入試において、優遇措置が取られるというメリットがあります。
(入試優遇措置の詳細については数学検定の公式ウェブサイトや各学校の入試に関する情報をご確認ください)
ここでは数学検定を「算数検定(6級~11級)」、「数学検定(3級~5級)」、「数学検定(準1級~2級)」の三つに分け、検定の概要をお伝えします。

実用数学技能検定(以下、数学検定と略す)は公益財団法人日本数学検定協会が実施する算数・数学の技能を測る記述式の検定であり、幼児から大学・一般レベルまで全15級の幅広い階級から構成されています。
個人の数学の技能を測ることはもちろんですが、それ以外にも検定に合格することで、学校によっては中学・高校・大学等の入試において、優遇措置が取られるというメリットがあります。
(入試優遇措置の詳細については数学検定の公式ウェブサイトや各学校の入試に関する情報をご確認ください)
ここでは数学検定を「算数検定(6級~11級)」、「数学検定(3級~5級)」、「数学検定(準1級~2級)」の三つに分け、検定の概要をお伝えします。
算数検定(6級~11級)について
算数検定(6級~11級)の内容は小学校で学ぶ算数について問われます。
5級以上の階級と異なり、1次・2次といった区分はありません。
検定の概要は表1・2の通りです。
各階級に目安となる小学校の学年を記しています。例えば6級は目安の学年が「小学6年程度」となっていますが、全ての問題が小学6年程度の内容で構成されているわけではなく、「小学6年程度」と「小学5年程度」の内容がそれぞれ45%ずつに加え、「特有問題」が10%で構成されています。
11級を除き6級~10級は同様の構成となっています。
難易度は出題範囲の内容の基本がしっかり身についていれば合格できるレベルです。
※ここでは表に掲載しませんでしたが、11級よりも下に「かず・かたち検定(GS・SS)」が存在しています。



数学検定(3級~5級)についてについて
5級より上の階級は1次と2次の二つの試験に分かれています。
1次は「計算技能検定」という名の通り計算技能を問う性質の問題であり、2次は「数理技能検定」といい数理応用技能を問う問題となっています。
1日で二つの試験を受け、1次または2次の片方にのみ合格するという場合もあります。
検定の概要は表3・4の通りです。各階級に目安となる中学の学年を記しています。
例えば3級は目安の学年が「中学3年程度」となっていますが、全ての問題が中学3年程度の内容で構成されているわけではなく、「中学1年程度」「中学2年程度」「中学3年程度」の内容がそれぞれ30%ずつに加え「特有問題」が10%で構成されています。
難易度は出題範囲の内容の基本がしっかり身についていれば合格できるレベルとなっています。
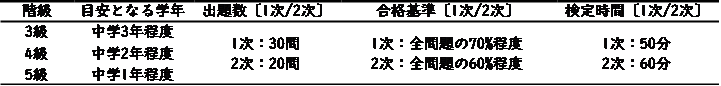

数学検定(準1級~2級)についてについて
準1級~2級も3級~5級と同じく1次「計算技能検定」と2次「数理技能検定」とに分かれていて、1日で二つの試験を受けます。1次または2次の片方にのみ合格するという場合もあります。
検定の概要は表5・6の通りです。各階級に目安となる高校の学年を記しています。
例えば準2級では目安の学年が「高校1年程度」となっていますが、全ての問題が高校1年程度の内容で構成されているわけではなく、「高校1年程度」の内容を50%、「中学3年程度」の内容を40%、それに「特有問題」10%を加え構成されています。
問題数について、準2級と3級を比較してみると、1次2次ともに問題数は半分となっており、級が上がると更に問題数は少なくなっていきます。
これは1問あたりの比重が高くなることを意味し、簡単に間違うことができません。
問題の難易度は基本的な問題で構成されており、高校の教科書レベルの内容をまずはしっかりと身につけ、その上で普段から教科書傍用問題集や網羅型問題集で勉強をしていれば十分合格レベルに達するでしょう。
ただし先程書いた通り、1問あたりの比重が高いため、苦手な単元を作らず出題範囲の内容を万遍なく学習することが大切です。
※ここでは表に掲載しませんでしたが、上に大学程度・一般レベルの1級が存在しています。


(参照・引用)数学検定 公式ウェブサイト
数学検定対策授業を随時行っています。ご希望の方はお問合せ下さい。(担当釼持)